This article is the first of a three-part series adapted from an essay written by Dr. Alex Berezow, which is now archived at Suzzallo Library's Special Collections at the University of Washington. In Part I, he discusses the most famous unsolved problem in mathematics, the Riemann Hypothesis.
Humans are problem solvers. Though our species name is Homo sapiens (Latin for “wise man”), perhaps a better one would be Homo problematis solvendis (“problem solving man”). If there’s a mountain, we’ll climb it; if there’s a moon, we’ll fly to it; if there’s a disease, we’ll cure it. Our species’ success in science and technology has even given rise to scientism1, the naïve and arrogant belief that science alone is the only legitimate source of knowledge and that any problem – no matter how great – will one day be solved by science.
It is easy to see why many people believe that. We are taught from a young age that the trickiest homework can be solved through diligent study; the toughest sporting competitions can be dominated through training; and the complexities of interpersonal relationships can be settled through understanding and compromise. All of this conspires to create in each of us a false sense that no problem is too big to tackle. Yet, the unfortunate reality is that, sometimes, no amount of thoughtfulness, hard work, or understanding will transform an intractable problem into a resolvable one. Indeed, some problems really have no solution.
The Riemann Hypothesis: A Mathematical Problem with No Solution?
Students of mathematics are well versed in the knowledge that some problems have no solutions. We learn in grade school that division by zero is simply impossible; the fabric of spacetime may unravel if we brazenly attempt such a feat. But this is more akin to a rule violation than a truly unsolvable problem. Are there legitimate mathematics problems that are so difficult that humans may never solve them?
Yes. In his excellent book The Millennium Problems: The Seven Greatest Unsolved Mathematical Puzzles of Our Time2, Keith Devlin describes what mathematicians agreed upon in Paris in the year 2000 as the biggest challenges facing the field. Most of them are far too advanced and esoteric for the average mathematician, let alone the average person. To make things interesting, the Clay Mathematics Institute offered a $1 million prize for each of the seven problems. Since then, only one has been solved – the Poincaré Conjecture, which involves the mathematical description of surfaces and, in Devlin’s words, demonstrate “the deep and fundamental ways in which a doughnut is the same as a coffee cup” – by Russian mathematician Grigoriy Perelman. Then, in stereotypically mysterious Russian fashion, he declined the $1 million prize, refused to give interviews, quit his job, retreated into obscurity, and moved in with his mother3. Perelman also declined the Fields Medal, which is the mathematical equivalent of the Nobel Prize.
For laymen, perhaps the most comprehensible of the seven (now six) problems is the Riemann Hypothesis, which deals with a topic that even the Ancient Greeks found fascinating: The prime numbers. Prime numbers are those numbers whose whole number factors include only 1 and itself. The first several prime numbers are 2, 3, 5, 7, 11, 13, 17, and 19. A number like 6 is composite, not prime, because it can be factored as 2 x 3. (As a side note, 6 is also a “perfect number,” because the whole number factors excluding itself – 1, 2, and 3 – sum to 6.) We know that there are fewer and fewer prime numbers the higher we go up the number line, and using a bit of logic, Euclid proved roughly 2300 years ago that the prime numbers go on infinitely. But modern-day mathematicians are not satisfied. They want to know if there is a pattern to the primes.
The answer to that question, if there is one, involves fairly sophisticated mathematics, such as taking the sum of an infinite series of numbers. Counterintuitive as it is, an infinite series of numbers can have a finite sum, as long as the series contains the “right kind” of numbers. For example, consider this infinite series:
s = 1 + x + x2 + x3 + x4…
Our intuition tells us that such a sum would be infinitely large, and it would be correct most of the time. However, if x = ½, then the infinite series of numbers has the modest and decidedly finite sum of 2.
As it turns out, a different infinite series of numbers, known as the zeta function, is intimately tied to the pattern of the primes.
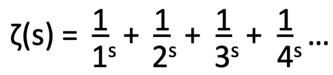
In his book, Devlin explains that in 1740, mathematician Leonhard Euler showed that the zeta function could be re-written in a very peculiar way.
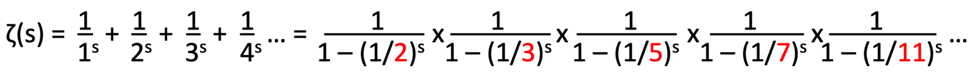
Thus, Euler directly linked the sum of an infinite series of numbers to the product of a different infinite series of numbers, whose terms consisted of denominators containing only the prime numbers. In 1859, Bernhard Riemann extended the concept to include imaginary numbers (i.e., those that contain the square root of -1, also known as i). Furthermore, he proposed that when the function equals 0, the solutions provide an insight into the distribution of the prime numbers. Specifically, he claimed that while there is an overall pattern to the prime numbers (namely, that they become less and less common), we cannot predict in advance which numbers will be prime.
This is known as the Riemann Hypothesis, and it is considered the greatest outstanding question in the field of mathematics. While mathematicians assume the hypothesis is true, it has not been proven in 160 years. Earlier this year, researchers reported possible progress toward a proof4, but that remains to be seen. It is entirely possible that the Riemann Hypothesis is true but unprovable, perhaps the most frustrating kind of problem for which there is no solution.
Read Part II: Aging and Cancer
Read Part III: Willful Ignorance
References
(1) Thomas Burnett. “What is Scientism?” American Association for the Advancement of Science. Accessed: 1-Oct-2019. https://www.aaas.org/programs/dialogue-science-ethics-and-religion/what-scientism
(2) Keith Devlin. The Millennium Problems: The Seven Greatest Unsolved Mathematical Puzzles of Our Time. 2006 edition. New York: Barnes & Noble.
(3) Dennis Overbye. “A Math Problem Solver Declines a $1 Million Prize.” New York Times. Published: 1-Jul-2010. Accessed: 25-Nov-2019. https://www.nytimes.com/2010/07/02/science/02math.html
(4) Emily Conover. “Mathematicians report possible progress on proving the Riemann hypothesis.” Science News. Published: 24-May-2019. Accessed: 27-Nov-2019. https://www.sciencenews.org/article/mathematicians-progress-riemann-hypothesis-proof

