Isn't it odd that Florida has so many people living with Alzheimer's Disease? If Erin Brockovich was investigating the case, she probably would conclude that it's something in the water.
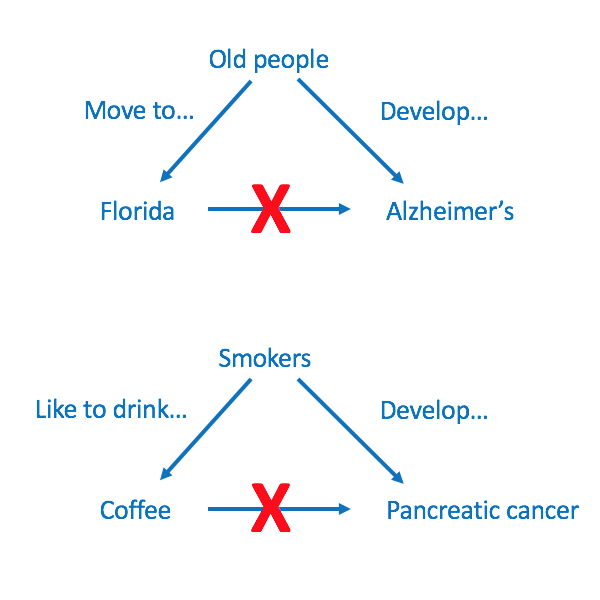
The rest of us, however, know that there's nothing especially dangerous about Florida.* Old people all across America move to Florida for retirement, and Alzheimer's is a disease associated with aging. Ergo, Florida is not causing Alzheimer's; aging is.
Using the vernacular of epidemiology, aging in this example is known as a confounding variable. The apparent association between living in Florida and having Alzheimer's is confounded by age. If a researcher did not take age into consideration, he would draw incorrect conclusions about a link between geography and Alzheimer's.
This is a relatively easy and intuitively obvious example, but confounding happens in all sorts of unexpected ways.
In 1981, a study (reported by the New York Times, of course) concluded that drinking coffee was linked to pancreatic cancer. The problem is that the authors didn't control for smoking. A lot of people who drink coffee also smoke. If the authors had adjusted their data for smoking, the link between coffee and pancreatic cancer would have vanished. The cigarettes, not the java, were causing pancreatic cancer, and meta-analyses since then have vindicated coffee.
Spurious Correlations
This example gets to the heart of all observational studies: One must use caution in concluding that A causes B because a third factor C may actually be to blame.
Sometimes, factor C is simply dumb luck. Consider this: The number of people who drowned in a swimming pool from 1999 to 2009 correlates with the number of movies in which Nicolas Cage appears. The number of letters in the winning word for the Scripps National Spelling Bee correlates with the number of people who were killed by venomous spiders. These and other spurious correlations, compiled by Tyler Vigen, hilariously demonstrate the folly of assuming A causes B if A correlates with B.
The internet savvy like to summarize this lesson as "correlation does not imply causation." But that, too, is wrong. We study correlations precisely because we are hoping to discover a causal effect. So, yes, correlations imply causation, but they are not sufficient to prove causation. For that, we need other evidence, such as biological mechanisms. There is no biologically plausible mechanism by which Nicolas Cage movies cause swimming pool drownings.
*Note: That is, except alligators and Florida Man.
