One of the major reasons scientific research is facing a reproducibility problem is because of poor use of statistics. In a bombshell 2005 article that still reverberates in the halls of academia (and industry), John Ioannidis used mathematics to coolly demonstrate why most published research findings are false1.
Statistics is difficult, and choosing the proper tools becomes more challenging as experiments become more complex. That's why it's not uncommon for large genetics or epidemiological studies to have a biostatistician as a co-author. Perhaps more biomedical studies should follow suit. One of Dr. Ioannidis's more recent findings shows that too many studies suffer from low statistical power2.
Two Types of Statistical Errors
There are two kinds of statistical errors, creatively called Type I and Type II.
Type I errors (also called alpha) are false positives. In a typical experiment in which two groups are being compared, a Type I error means that the researchers incorrectly conclude that a real difference exists between the groups. In reality, there is no difference. For example, if a clinical trial tests the efficacy of a drug compared to a placebo, the Type I error gives the probability that the scientists will conclude the drug is effective when it actually is not. Researchers usually set the Type I error rate at 5%, but the lower the number, the better.
Type II errors (also called beta) are false negatives, which means the researchers failed to detect a difference between the two groups when a difference actually existed. However, it is more useful to think of Type II errors in the form of statistical power, expressed as (1 - beta). Statistical power expresses the likelihood that, if a real difference exists, the researchers will be able to find it. Researchers should aim for 80% power, but the higher the number, the better.
Why is low statistical power a problem? A paper in the journal Royal Society Open Science explains:
Studies with low statistical power increase the likelihood that a statistically significant finding represents a false positive result... [A]ssuming a threshold for declaring statistical significance of 5%, we found that approximately 50% of studies have statistical power in the 0–10% or 11–20% range, well below the minimum of 80% that is often considered conventional.
This is very bad. Dr. Ioannidis shows that a study with a statistical power of 20% will come to the wrong conclusion about 50% of the time. But the good news is that it's fixable. If scientists plan ahead correctly, they can determine the sample sizes they need in order to deliver statistically convincing results. And a tool to do just that exists.
G*Power to the People
Several years ago, German researchers developed free software, called G*Power, that calculates sample size. Every scientist should use it.
Let's pretend that we are doing a study in mice, and we are comparing some chemical with a placebo to determine toxicity. We may choose a common statistical design, called a two-sided t-test. We set Type I error at 5% and statistical power at 80%. Because we want to reliably detect very tiny differences between the two groups of animals, we choose an effect size of 0.2. How many animals do we need in our study?
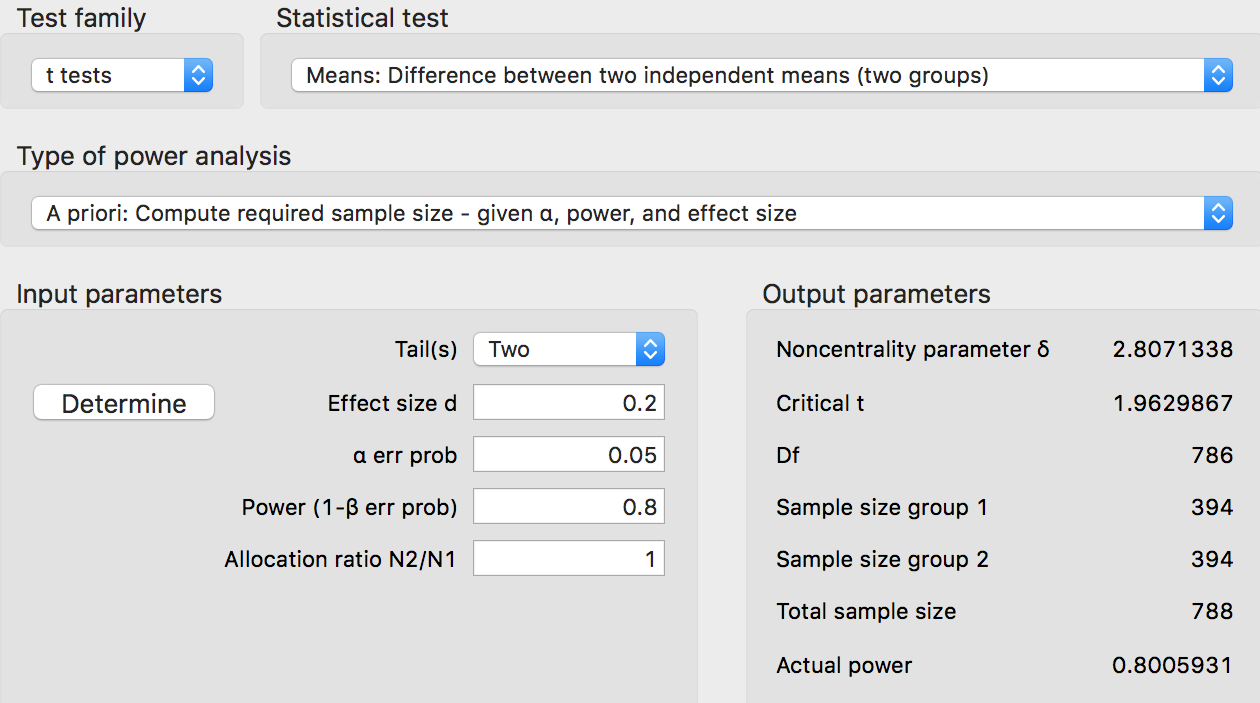
Whoa! G*Power says we need 394 mice... per group. Most mouse studies use 10 or 20 per group. That's fine, because animals are expensive (and we want to use as few as absolutely necessary), but it comes with a very important caveat: Studies with small sample sizes cannot reliably detect small differences. To detect small differences, studies must have large sample sizes.
To improve the reliability of scientific research, we must insist on appropriate sample sizes. And journalists who write about the latest "scary chemical" or "miracle cure" should learn about them.
Notes
(1) Dr. Ioannidis is perhaps the most famous, but not the first, to note this. Jacob Cohen began examining the problem in 1962.
(2) Dr. David Streiner, co-author of the textbook Biostatistics: The Bare Essentials, argues that it is impossible to do an after-the-fact calculation of statistical power. He also believes that several of Dr. Ioannidis's claims are based on a flawed understanding of significance at a level of 5%.




